Kdyz ji miluješ.....
...není co řešit
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Vítejte na blogu allstar teamu věnováný výhradně
kvalitní (velmi kvalitní) matematice 
Pozn.: Tento blog byl vytvořen za účelem úspěšného zvladnutí matematických nástrah a výzev, jež stojí před tímto týmem (allstar) v jeho cestě nelehké, za kýženým vzděláním a poznáním všehomíra. Budiž jim Matematika v ekonomii milostivá. Ámen
© All rights reserved
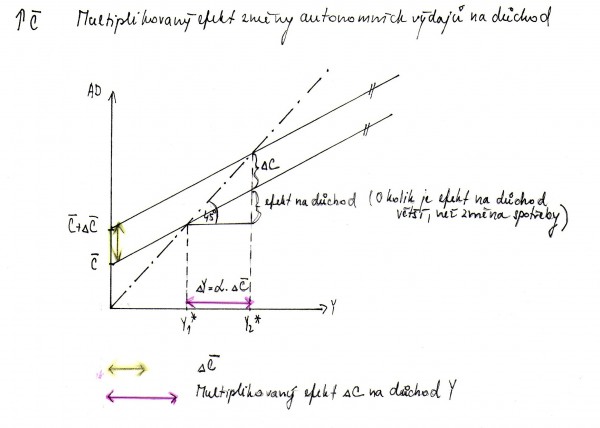
Vliv změny sklonu na důchod
Elasticita funkce v bodě
Grafy funkcí
Na následujícím odkaze naleznete průběhy základních funkcí
Pomůcka pro matematicky méně zdatné
Asi pobavím nejen ostatní členy našeho allstar teamu, ale minulý týden jsem se na přednášce přistihla, že mi stále, nebo spíše už zase dělá problém dosazování výrazu ∞ do čitatele a jmenovatele zlomků ve vzorcích. Ať už na tento banální problém narážím v matematice nebo v ekonomii, musím si v tom pro jednou udělat jasno! J
∞ + 2 = ∞
∞ - 3 = ∞
∞ * 2 = ∞
∞ * (-3) = - ∞
- ∞ * 2 = - ∞
- ∞ * (-4) = ∞
- ∞ + 2 = - ∞
- ∞ - 3 = - ∞
∞ = ∞
2
∞ = - ∞
-2
- ∞ = - ∞
3
- ∞ = ∞
- 4
Je definováno: Není definováno = neurčité výrazy:
∞ + ∞ = ∞ ∞ - ∞
- ∞ - ∞ = - ∞ - ∞ + ∞
∞ * ∞ = ∞ ± ∞ * 0
- ∞ * ∞ = - ∞ ± ∞
± ∞
- ∞. (- ∞) = ∞ 00 , 1± ∞ , (± ∞)0
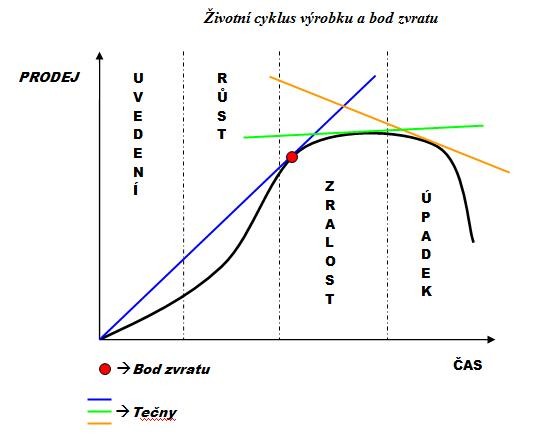
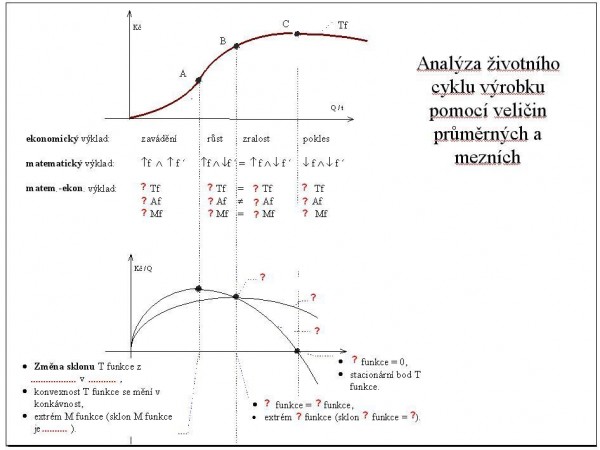
Analýza životního cyklu výrobku
Zdravím všechny matematické nadšence allstar teamu:-)
Už jste si zkoušeli slepý obrázek "analýza životního cyklu výrobku pomocí veličin průměrných a mezních"? Není to tak zlé a věřím, že když si to párkrát vyzkouším, na písemce se mi to pak vybaví samo:-) Tady je jedna z možných variant, jak by to asi mohlo vypadat.
Záměna os
Další příspěvek se věnuje záměně os v grafu. Praxe je většinou taková, že na vodorovné ose znározňována nezávislá proměnná (X) a na svislé ose závisle proměnná (Y), alespoň tak nám to vštěpovali učitelé na elektrotechnické průmyslovce, kterou jsem 4 roky navštěvoval. Po příchodu na ekonomickou fakultu, bylo vše jinak, jelikož lze v ekonomii potažmo v grafech zobrazujících různé ekonomické závislosti, mít nezávisle proměnnou na svislé ose grafu.
Typickým příkladem může být křivka poptávky např. po penězích..., kde na vodorovné ose je množství peněz a na svislé ose je úroková míra (=> vyjadřuje cenu peněz). Čím je vyšší úroková míra, tím méně budeme poptávat peněz (bude růst jejich cena) a čím nižší úroková míra, tím budeme peněz poptávat více (cena peněz bude klesat). z toho plyne, že množství peněz se odvíjí od jejich ceny potažmo úrokové míry, kdybychom vyměnili tyto vzájemné závislosti, racionálně smýšlející člověk by se nerozhodoval o poptávaném množství peněz na základě jejich ceny (úrokové míry).

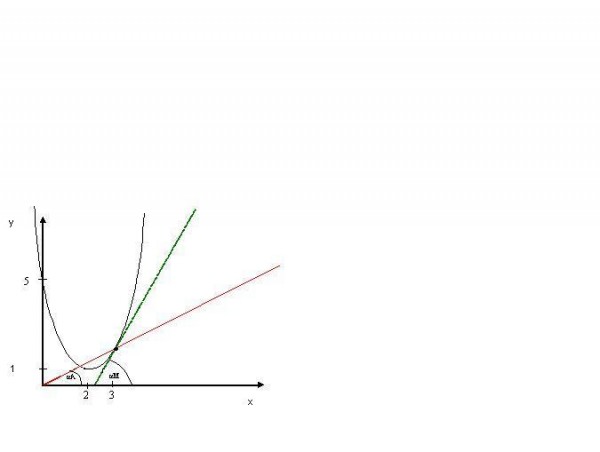
Jak se hledá tečna ke grafu funkce?
Abychom mohli řešit příklad tohoto typu, potřebujeme znát zadání funkce [ y =f(x) ] a tečný bod T[ x; y ]. Celý postup se nejlépe bude vysvětlovat na "skutečném" příkladu, proto si nyní zadejme konkrétní hodnoty:
Hledání bodu zvratu - DÚ
Zadání: K funkci uvedené v prezentaci s názvem Veličiny celkové, průměrné a mezní (Podklady k přednášce) z repozitory, a to na snímku č. 22 této prezentace, je uvedena funkce celkových veličin. Na obrázku jsou znázorněny k ní příslušné funkce veličin průměrných a mezních.
Životní cyklus výrobku a bod zvratu
Bod zvratu lze zjistit prostřednictvím matematického výpočtu nebo prostřednictvím grafického znázornění. V případě použití grafického aparátu, mužeme bod zvratu nalézt tak, že vedeme z počátku tečnu, místo kde se tečna dotýká grafu pouze v jednom bodě nazýváme bod zvratu, v obrázku jsou nakresleny i některé další tečny, které se pohybují po daném grafu a neprocházejí počátkem.