|
2. listopad 2009 v 17.25 | rubrika: Petra Lelková
snížení mpc početně:
α1 = ?, c1 = 0,5
α2 = ?, c2 = 0,3
___________
α1 = 1____ = 1____ = 1__ |
přečteno: 66x | komentáře (1)
|
|
Odvození vzorce multiplikátoru α
2. listopad 2009 v 17.12 | rubrika: Petra Lelková
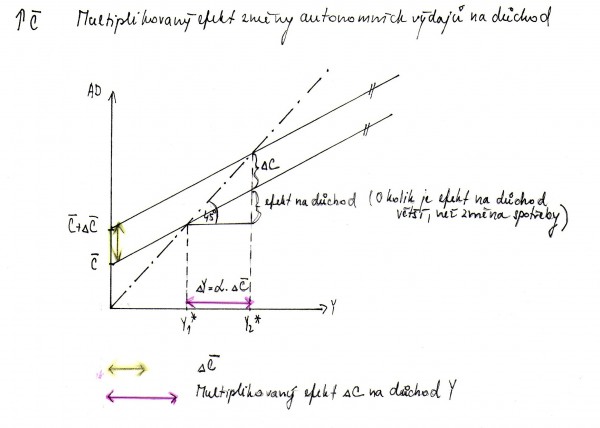  |
přečteno: 218x | přidat komentář
|
|
Elasticita funkce v bodě
17. říjen 2009 v 20.13 | rubrika: Petra Lelková
y = (x-2)2 + 1
V = [2;1]
průsečík s osou y: xà0
y= (0-2)2 + 1=5
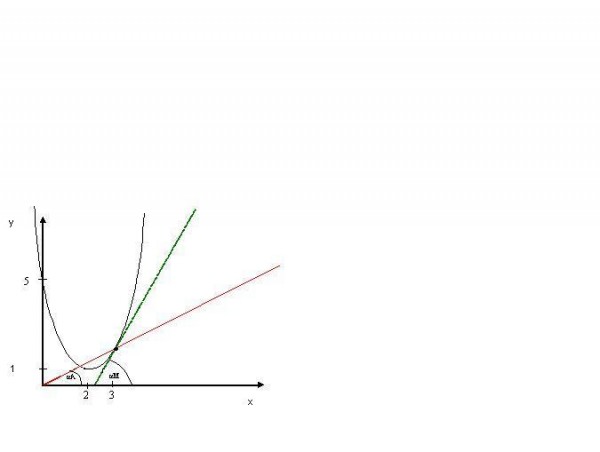
Určení elasticity funkce v bodě x=3
Grafické určení elasticity podle velikosti úhlů:
|E(3)|= αA < αM à tg αA < tg αM à
tg αM
tg αA > 1
Funkce je v bodě x=3 elastická
|
přečteno: 374x | přidat komentář
|
|
Grafy funkcí
15. říjen 2009 v 18.45 | rubrika: Aleš Grym
Na následujícím odkaze naleznete průběhy základních funkcí |
přečteno: 58x | přidat komentář
|
|
Pomůcka pro matematicky méně zdatné
6. říjen 2009 v 15.28 | rubrika: Petra Lelková
Asi pobavím nejen ostatní členy našeho allstar teamu, ale minulý týden jsem se na přednášce přistihla, že mi stále, nebo spíše už zase dělá problém dosazování výrazu ∞ do čitatele a jmenovatele zlomků ve vzorcích. Ať už na tento banální problém narážím v matematice nebo v ekonomii, musím si v tom pro jednou udělat jasno! J ∞ + 2 = ∞ ∞ - 3 = ∞ ∞ * 2 = ∞ ∞ * (-3) = - ∞ - ∞ * 2 = - ∞ - ∞ * (-4) = ∞ - ∞ + 2 = - ∞ - ∞ - 3 = - ∞ ∞ = ∞ 2 ∞ = - ∞ -2 - ∞ = - ∞ 3 - ∞ = ∞ - 4 Je definováno: Není definováno = neurčité výrazy: ∞ + ∞ = ∞ ∞ - ∞ - ∞ - ∞ = - ∞ - ∞ + ∞ ∞ * ∞ = ∞ ± ∞ * 0 - ∞ * ∞ = - ∞ ± ∞ ± ∞ - ∞. (- ∞) = ∞ 00 , 1± ∞ , (± ∞)0
|
přečteno: 43x | komentáře (2)
|
|
Analýza životního cyklu výrobku
2. říjen 2009 v 23.00 | rubrika: Marie Hradilová
Zdravím všechny matematické nadšence allstar teamu:-) Už jste si zkoušeli slepý obrázek "analýza životního cyklu výrobku pomocí veličin průměrných a mezních"? Není to tak zlé a věřím, že když si to párkrát vyzkouším, na písemce se mi to pak vybaví samo:-) Tady je jedna z možných variant, jak by to asi mohlo vypadat. 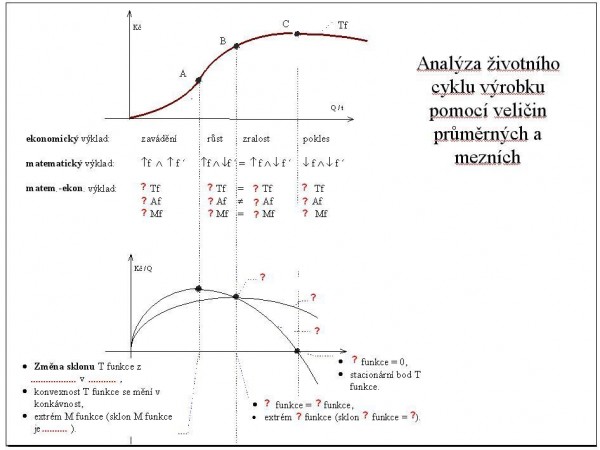 |
přečteno: 397x | přidat komentář
|
|
Záměna os
2. říjen 2009 v 14.18 | rubrika: Aleš Grym
Další příspěvek se věnuje záměně os v grafu. Praxe je většinou taková, že na vodorovné ose znározňována nezávislá proměnná (X) a na svislé ose závisle proměnná (Y), alespoň tak nám to vštěpovali učitelé na elektrotechnické průmyslovce, kterou jsem 4 roky navštěvoval. Po příchodu na ekonomickou fakultu, bylo vše jinak, jelikož lze v ekonomii potažmo v grafech zobrazujících různé ekonomické závislosti, mít nezávisle proměnnou na svislé ose grafu. Typickým příkladem může být křivka poptávky např. po penězích..., kde na vodorovné ose je množství peněz a na svislé ose je úroková míra (=> vyjadřuje cenu peněz). Čím je vyšší úroková míra, tím méně budeme poptávat peněz (bude růst jejich cena) a čím nižší úroková míra, tím budeme peněz poptávat více (cena peněz bude klesat). z toho plyne, že množství peněz se odvíjí od jejich ceny potažmo úrokové míry, kdybychom vyměnili tyto vzájemné závislosti, racionálně smýšlející člověk by se nerozhodoval o poptávaném množství peněz na základě jejich ceny (úrokové míry).

|
přečteno: 121x | přidat komentář
|
|
2. říjen 2009 v 14.00 | rubrika: Jana Juríková
Abychom mohli řešit příklad tohoto typu, potřebujeme znát zadání funkce [ y =f(x) ] a tečný bod T[ x; y ]. Celý postup se nejlépe bude vysvětlovat na "skutečném" příkladu, proto si nyní zadejme konkrétní hodnoty: |
přečteno: 12.740x | komentáře (10)
|
|
27. září 2009 v 19.01 | rubrika: Marie Hradilová
Zadání: K funkci uvedené v prezentaci s názvem Veličiny celkové, průměrné a mezní (Podklady k přednášce) z repozitory, a to na snímku č. 22 této prezentace, je uvedena funkce celkových veličin. Na obrázku jsou znázorněny k ní příslušné funkce veličin průměrných a mezních. |
přečteno: 250x | komentáře (1)
|
|
Životní cyklus výrobku a bod zvratu
27. září 2009 v 15.30 | rubrika: Aleš Grym
Bod zvratu lze zjistit prostřednictvím matematického výpočtu nebo prostřednictvím grafického znázornění. V případě použití grafického aparátu, mužeme bod zvratu nalézt tak, že vedeme z počátku tečnu, místo kde se tečna dotýká grafu pouze v jednom bodě nazýváme bod zvratu, v obrázku jsou nakresleny i některé další tečny, které se pohybují po daném grafu a neprocházejí počátkem.
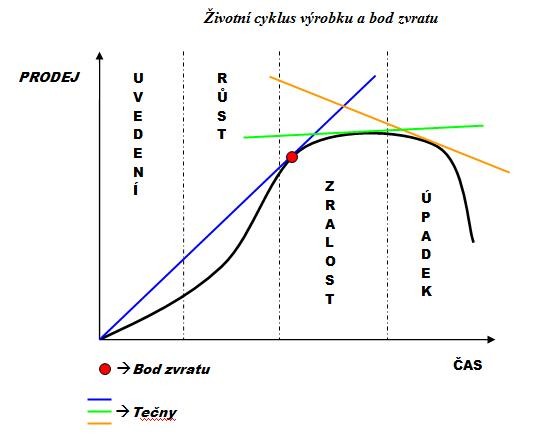 |
přečteno: 1.327x | přidat komentář
|